Brief
The application of scientific methods to the study of operations of large complex organizations or activities in order to give executives a quantitative basis for reaching optimum decisions
Sample Questions (Applications)
Reddy Mikks produces both interior and exterior paints from two raw materials, M1 and M2. The following table provides the basic data of the problem:
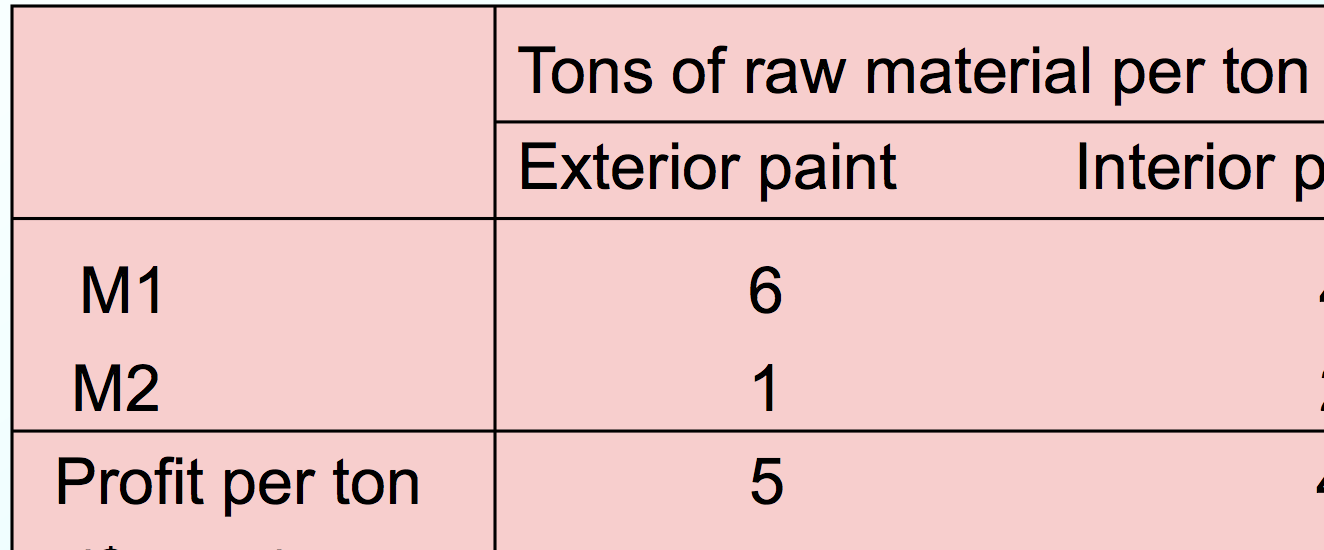
How to achieve the maximum profit ?
Steps:
- Problem Definition and Data Gathering
- Mathematical Model Building (introduce below)
- Developing Solution Approach
- Model Solution Testing
- Implementation
Finding Jobs’
- Decision variable: No. of M1, x1 and No. of M2, x2
- Objective: Maximum profit
- Constraint: Limitation of the materials
Mathematic descriptiong
- Decision variable:
- X1 = Tons produced daily of exterior paint
- X2 = Tons produced daily of interior paint
- Objective function: _Maximize the total daily profit (z)
- z=5*X1 + 4*X2
- Constraint:
- 6*X1 + 4*X2 ≤ 24 ( Raw material M1)
- X1 + 2*X2 ≤ 6 (RawmaterialM2)
Methods
- Graphical Solution Method ( for 2 decision variables problem, we can draw a graphy and slove it. )
- Simplex Method ( a general solution technique for solving LP problem. introduce below. )
Simplex Method
Definition
- Extreme point solution (corner point solution): Solution points that lie on the intersection of a number of constraint lines.
- Adjacent Extreme point solution: Two extreme point solutions are adjacent extreme points if they are connected by a constraint line (2-dimension case).
- An optimal solution is always a corner point solution and none of the adjacent extreme point solution is better off in the value of the objective function.