一元线性回归

上接 应用工程统计学基础

• 简介
• 模型和假设
• 由样本来估计模型的参数
  • 一般使用最小二乘法，估计$\beta_{0}，\beta_{1}$
  • 然后估计$\sigma^{2}$
  • 问题产生了：这些估计值好不好?
  • 分析 $\hat{\beta}_{1}$
  • 用$\hat{\beta}_{1}$来判断x和y是否线性相关!
  • 分析$\hat{\beta}_{0}$, 虽然其实大家并不怎么关心$\beta_{0}$
• 模型整体评估
  • 评估策略一： R-Square
  • 评估策略二： 方差分析 ANOVA
• 模型充分性检查
  • 开头我们列举了关于误差的假设，一般画图表判断
• 分析一下y的置信区间
  • 分析$\mu_{Y|x}$的期望值和方差

简介

一元线性回归预测是指成对的两个变量数据的散点图呈现出直线趋势时，采用最小二乘法，找到两者之间的经验公式，即一元线性回归预测模型。

• 回归分析：对两个不确定关系的变量进行统计学分析建模。（回归一般理解为向均值回归）
• 经验公式：根据观察推断出公式，而不是根据理论。

模型和假设

一元线性回归模型 $Y=\beta_{0}+\beta_{1}x+\varepsilon$ 包括两个部分

• 确定性部分，$y=\beta_{0}+\beta_{1}x$
• 不确定性部分，误差 $\varepsilon$。

对误差的假设（之后讨论如何对误差进行分析，见模型充分性检查）

• 所有误差$\varepsilon_{1}...\varepsilon_{n}$都是随机和独立的
• 所有误差$\varepsilon_{1}...\varepsilon_{n}$均值为0
• 所有误差$\varepsilon_{1}...\varepsilon_{n}$有相同方差$\sigma^{2}$
• 所有误差$\varepsilon_{1}...\varepsilon_{n}$呈正态分布

基于对误差的假设，我们可以知道，在任意一个$x_{i}$点上，$Y_{i}$的值都服从相同方差（形状）的正态分布。

• $Y_{i}$期望值：$E(Y_{i})=E(\beta_{0}+\beta_{1}x_{i}+\varepsilon_{i})=\beta_{0}+\beta_{1}x_{i}+E(\varepsilon_{i})=\beta_{0}+\beta_{1}x_{i}$
• $Y_{i}$方差：$V(Y_{i})=V(\beta_{0}+\beta_{1}x_{i}+\varepsilon_{i})=V(\varepsilon_{i})=\sigma^{2}$

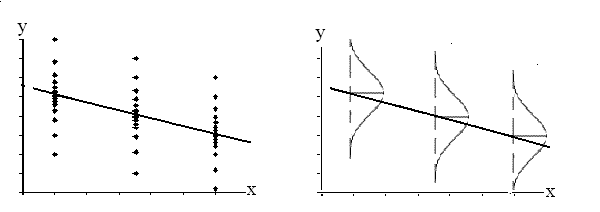
由样本来估计模型的参数

一般来说，$\beta_{0}和\beta_{1}$都是未知的，我们可以根据样本来估计他们的值。
既然是估计值，大家都戴上帽子，等式变为$\hat{Y}=\hat{\beta}_{0}+\hat{\beta}_{1}x$

一般使用最小二乘法，估计$\beta_{0}，\beta_{1}$

找出$\hat{\beta}_{0}和\hat{\beta}_{1}$使总的误差平方和最小。即$Minimize\;f(\hat{\beta}_{0},\hat{\beta}_{1})=\sum_{i=1}^{n}\varepsilon_{i}^{2}=\sum_{i=1}^{n}(y_{i}-\hat{\beta}_{0}+\hat{\beta}_{1}x_{i})^{2}$
求极值，进行求导，运算，得到结果：
$\hat{\beta}_{0}=\bar{y}-\hat{\beta}_{1}\bar{x}$
$\hat{\beta}_{1}=\frac{S_{xy}}{S_{xx}}$
于是我们可以先求得$\hat{\beta}_{1}$，再求得$\hat{\beta}_{0}$。

然后估计$\sigma^{2}$

我们定义$SSE=\sum_{i=1}^{n}e_{i}^{2}=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}$。
那么$\hat{\sigma}^{2}=MSE=\frac{SSE}{N-2}$ （因为失去两个自由度$\hat{\beta}_{0}，\hat{\beta}_{1}$）

问题产生了：这些估计值好不好?

我们知道$\hat{\beta}_{0}，\hat{\beta}_{1}$是根据样本计算出来的估计值，那么根据同一总体的不同的样本我们会得到不一样的$\hat{\beta}_{0}，\hat{\beta}_{1}$。

分析 $\hat{\beta}_{1}$

因为$\varepsilon_{i}$服从正态分布，所以$y_{i}$服从正态分布，由于$\hat{\beta}_{1}=\frac{S_{xy}}{S_{xx}}，\hat{\beta}_{1}和y_{i}们为线性关系$，我们得出：

• $\hat{\beta}_{1}$服从正态分布
• 期望值 $E(\hat{\beta}_{1})=\beta_{1}$

• 方差 $Var(\hat{\beta}_{1})=\sigma_{\hat{\beta}_{1}}^{2}=\frac{\sigma^{2}}{\sum (x_{i}-\bar{x})^{2}}=\frac{\sigma^{2}}{S_{xx}}$.

  从方差等式$Var(\hat{\beta}_{1})=\frac{\sigma^{2}}{\sum (x_{i}-\bar{x})^{2}}$中，我们可以知道，为了减小$\hat{\beta}_{1}$的方差，从分母上看，拿更大的样本，分母会变得更大，能有效减小$Var(\hat{\beta}_{1})$。当然在相同条件下，样本x点在合理范围内分布更广的话，势必$\sum (x_{i}-\bar{x})^{2}$也会更大。

用$\hat{\beta}_{1}$来判断x和y是否线性相关!

既然知道了$\hat{\beta}_{1}～N(\beta_{1},\sigma^{2}/S_{xx})$，我们可以进行假设检验。
用T-test来假设验证他的均值$H_{0}: \beta_{1} = 0$, 如果无法拒绝$\beta_{1}$等于零，则意味着无法肯定x和y的线性关系。
$H_{0}: \beta_{1} = 0$
$H_{1}: \beta_{1} \neq 0$
测试的统计量:
$T_{0}=\frac{\hat{\beta}_{1}-0}{\hat{\sigma}/\sqrt{S_{xx}}}$
检验方式：1.P值 2.给定显著性水平 3.置信区间
（我们在用工具建立线性回归模型时候，工具都会帮我们自动进行这个T检验，以判断x和y的线性关系是否significant。）

分析$\hat{\beta}_{0}$, 虽然其实大家并不怎么关心$\beta_{0}$

因为$\hat{\beta}_{1}$服从正态分布，然后$\hat{\beta}_{0}$和他是线性关系，所以$\hat{\beta}_{0}$也是服从正态分布。
$\hat{\beta}_{0}～N(\beta_{0},\sigma_{\hat{\beta}_{0}}^{2})$

模型整体评估

评估策略一： R-Square

线性回归模型的整体评估用了一个很有趣的思路，$R^{2}$，我们看模型解释了多少的方差，具体如下

• 模型方差 $SSE=\sum_{i=1}^{n}(e_{i}^{2})=\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}$
• 样本整体方差 $SST=\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}$

然后$R^{2}=1-\frac{SSE}{SST}$，这个值高意味着我们的模型消除了y的不确定性，这个值低则意味着我们的模型不好。
在模型输出中，一般我们还可以看到修正以后的$R_{adj}^{2}=1-\frac{MSE}{MST}=1-\frac{SSE/(n-2)}{MST/(n-1)}$，会比$R^{2}$小一点点，毕竟n-2 < n-1 （对一元模型来说这个值不重要，在多元模型中就不仅仅是n-2了，那是n-k-1，对多元模型来说这个值同时考虑了精准度和模型复杂程度，在我们取舍$x_{i}$的时候有用处。）

评估策略二： 方差分析 ANOVA

对等式稍微做一下变形$R^{2}=1-\frac{SSE}{SST}=\frac{SST-SSE}{SST}=\frac{SSR}{SST}$，SSR是regression模型解释的方差。
即$SS_{T}=\sum_{i=1}^{n}(y_{i}-\bar{y})^{2}=\sum_{i=1}^{n}(\hat{y}_{i}-\bar{y})^{2}+\sum_{i=1}^{n}(y_{i}-\hat{y}_{i})^{2}=SS_{R}+SS_{E}$
$\color{red}{如果\beta_{1}=0， 则用最小二乘法得出的等式将会是y=\bar{y},即x和y线性无关，则方差相等，是最小二乘法得到的结果里面的最坏情况了。}$ 于是我们用ANOVA来假设检验两个方差是否相等，如果模型能解释的方差大于不能被模型解释的方差，那我们认为这个模型是有效的。
既然SST的自由度为n-1，SSE的自由度为n-2，SST=SSR+SSE，SSR的自由度就是1了。
F验证：
$H_{0}: \sigma_{1}^{2} = \sigma_{2}^{2}$
$H_{1}: \sigma_{1}^{2} > \sigma_{2}^{2}$
测试的统计量：
$F_{0} = \frac{\frac{SST}{(a-1)}}{\frac{SSE}{a(n-1)}}=\frac{MSE}{MSE} ～ F_{1,n-2}$
检验方式：1.P值 2.给定显著性水平 3.置信区间.

模型充分性检查

开头我们列举了关于误差的假设，一般画图表判断

• 误差分析图，看看误差的分布情况 $e_{i} = y_{i}-\hat{y}_{i}$
• 正态概率图，看看误差是不是呈正态分布

分析一下y的置信区间

在这里，我们用$x^{*}$代表自变量x的一个指定值。
当$x=x^{*}$时，Y的期望值或均值表示为： $\mu_{Y|x}$
当$x=x^{*}$时，Y的预测值表示为： $Y|x$

分析$\mu_{Y|x}$的期望值和方差

$E(\hat{\mu}_{Y|x^{*}}) = E(\hat{Y}) = E(\hat{\beta}_{0} + \hat{\beta}_{1}x^{*}) = \beta_{0} + \beta_{1}x^{*}$
$Var(\hat{\mu}_{Y|x^{*}}) = \sigma^{2}[\frac{1}{n} + \frac{(x^{*}-\bar{x})^{2}}{\sum_{j=1}^{n}(x_{j}-\bar{x}^{2})}]$

未完待续。。。