应用工程统计学基础

• 基本概念
• 连续型随机变量
  • 那怎样定义概率？
  • 平均值和方差 Mean and Variance
  • 重要的连续型随机变量分布：
• 离散型随机变量
  • 定义概率
  • 平均值和方差 Mean and Variance
  • 重要的离散分布：
• 中心极限定理 The Central Limit Theorem
• 单样本情况
  • 统计推断
  • 参数估计
  • 假设检验
  • P值(P-Value)
  • 均值的置信区间 Confidence Interval on the Mean
  • 单个样本问题主要有以下几种情况
• 双样本情况
  • 在总体方差已知的情况下，推测两个分布均值的差别
  • 在总体方差未知的情况下，推测两个分布均值的差别
  • 配对样本t检验 Paired t-Test
  • 两个正态分布变量的总体方差是否相等
• 多样本情况（ANOVA）

基本概念

随机变量 是指变量的值无法预先确定，仅以一定的可能性(概率)取值的量。

• 连续型随机变量： 对于随机变量X，若存在一个非负的可积函数f(x)，使得对任意实数x，有 $\int_{-\infty }^{x}f\left ( u \right )du$，则称X为连续性随机变量。
• 离散型随机变量： 取值只有有限个或可列无穷个。

概率 是出现某个值的可能性。

连续型随机变量

对于连续型变量，它的值是无限的，于是对于某个点来讲，它的概率是零，即P(X=x)=0

那怎样定义概率？

• 概率密度函数: Probability Density Function (pdf)
  $P(a<X<b)=\int_{a}^{b}f(x)dx\quad 其中： 1. f(x) \geq 0 \quad 2.\int_{- \infty }^{ \infty }f(x)dx = 1$

• 累积分布函数: Cumulative Distribution Function (cdf)
  $F\left ( x \right ) = P(X \leq x) = \int_{-\infty }^{x}f\left ( u \right )du$

平均值和方差 Mean and Variance

平均值 (期望值)： $\mu = E(X) = \int_{-\infty }^{\infty} xf(x)dx$
方差： $\sigma ^{2} = V(X) = \int_{-\infty }^{\infty} (x - \mu)^2 f(x)dx = E(X^2 ) - \mu^2$
标准方差为 $\sigma$

重要的连续型随机变量分布：

正态(Normal)分布 又名高斯(Gaussian)分布 Normal Distribution

为什么重要： 中心极限定理 The Central Limit Theorem*
怎么来的: 正态分布的前世今生
表示成： $X \sim \mathcal{N}(\mu,\,\sigma^{2})\,$
它的概率密度函数为： $f(x) = \frac{1}{\sqrt{2\pi \sigma ^{2}}} \mathrm{exp}\left ( - \frac{ \left ( x - \mu \right )^{2}}{2\sigma ^{2}} \right ) 其中： \mu \mathbb\in {R},\sigma ^{2} > 0$
$\mu 是平均值， \sigma ^{2}是方差$

标准正态分布 Standard Normal Distribution

当一个正态分布变量满足$均值\mu = 0， 方差\sigma ^{2} = 1$， 我们把它称为标准正态分布变量，记做 ‘Z’ 。

• 它的概率密度函数为：$f(x) = \frac{1}{\sqrt{2\pi}} \mathrm{exp}\left ( - \frac{x^{2}}{2} \right )$
• 它的累积分布函数为：$\Phi\left ( z \right ) = \mathbb{P}\left [ Z \leq z \right ]$

如果X是一个普通的正态分布变量，$平均值为\mu， 方差为\sigma ^{2}$，我们可以将其 转化 为标准正态分布变量：
$Z = \frac{X - \mu }{\sigma }$
所以：
$\mathbb{P}\left [ X\leq x \right ] = \mathbb{P}\left [ \frac{X - \mu }{\sigma } \leq \frac{x - \mu }{\sigma } \right ] = \Phi \left ( \frac{x - \mu }{\sigma } \right )$
然后我们就可以使用标准正态分布表查询概率了，表上面是它的累积分布函数的值。

离散型随机变量

取值只有有限个或可列无穷个，比如投骰子的点数，调查的人数。

定义概率

• 概率质量函数 Probability Mass Function: 离散随机变量在各特定取值上的概率
  $f(x_{i}) = P(X = x_{i})$

• 累积分布函数: Cumulative Distribution Function
  $F(x) = P(X \leq x) = \sum_{x_{i} \leq x}^{} f(x_{i})$

平均值和方差 Mean and Variance

平均值 (期望值)： $\mu = E(X) = \sum_{i=1}^{n} x_{i}f(x_{i})$
方差： $\sigma ^{2} = V(X) = E(X-\mu)^2 = \sum_{i=1}^{n} (x_{i} - \mu)^2f(x_{i}) = \sum_{i=1}^{n}x_{i}^2f(x_{i}) -\mu^2$
标准方差为 $\sigma$

重要的离散分布：

二项分布 Binomial Distribution 又名贝努利（Bernoulli）分布

只有两种可能结果（0或1，成功或失败）的试验非常频繁，我们将它们称为贝努利试验。
基于假设： 1. 每一次试验都是独立的，不会受到其他试验的影响。 2. 试验为某一值的概率是恒定的。
比如著名的抛硬币实验，结果只有正面和反面，每一次投硬币都是独立的，为正面和反面的概率都恒定是0.5。

n次二项分布试验的结果中某一值出现的个数的几率
$f(x) = \binom{n}{x} p^{x} (1-p)^{n-x}, x = 0,1,...,n$

中心极限定理 The Central Limit Theorem

在一定条件下，大量独立随机变量的平均数是以正态分布为极限的。即你多次从总体中拿样本，只要样本数量n足够大，分别计算它们的均值，这些均值的分布趋于正态分布。$\mu_{X}=\mu_{x},\sigma(X)=\sigma(x)/\sqrt{N}$。推导
有趣的是： 无论是属于什么分布的随机变量，都满足这个定理。

于是我们得到关于样本均值$\bar{X}$的标准正态分布函数：
$\color{red}{Z = \frac{\bar{X} - \mu }{\sigma / \sqrt{n}} \quad as \quad n \to \infty }$ (后面会经常用到这个公式)

单样本情况

统计推断

统计在研究现象的总体数量关系时，需要了解的总体对象的范围往往是很大的，有时甚至是无限的，而由于经费、时间和精力等各种原因，以致有时在客观上只能从中观察部分单位或有限单位进行计算和分析，我们要根据样本数据来推断总体数量特征。
统计推断分为两个部分： 参数估计和假设检验

参数估计

• 一般用样本均值估计总体均值
  样本均值函数: $\mu = \frac{\sum_{i=1}^{N}x_{i}}{N}$

• 一般用样本方差估计总体方差
  样本方差： $s^{2} = \frac{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}{n-1} \quad (由于\bar{x}是由x_{i}计算出来的值，所以自由度为n-1)$
  总体方差： $\sigma^{2} = \frac{\sum_{i=1}^{N}(x_{i}-\mu)^{2}}{N}$

点估计

未知参数 $\theta$	统计 $\hat{\Theta}$	点估计 $\hat{\theta}$
$\mu$	$\bar{X}= \frac{\sum X_{i}}{n}$	$\bar{x}$
$\sigma^{2}$	$S^{2}=\frac{\sum (X_{i} - X)^{2}}{n-1}$	$s^{2}$

假设检验

基本思想是小概率反证思想。小概率事件（P<0.01或P<0.05）在一次试验中基本上不会发生。
即我们对总体的某个统计量（一般为均值）提出零假设H0，然后求得在这个零假设前提下当前样本的发生概率，如果概率非常小，则认为我们的零假设不对，拒绝我们的零假设H0。
具体步骤结合例子为下面7步：
例子： 我们想知道一种固体推进器的线性燃烧速率是否为50cm/s，前提假设总体方差已知为2.5。于是我们做了试验，得到一组样本数据，然后我们进行假设检验：

1. 将问题提炼为统计问题: $\color{red}{我们关心的是总体均值 \mu是否为50cm/s}$
2. 提出零假设 Null hypothesis, $\color{red}{ H_{0}: \mu=50cm/s }$
3. 提出备择假设 Alternative hypothesis, $\color{red}{ H_{1}: \mu\neq 50cm/s }$
4. 确立检验统计量: $\color{red}{样本均值 \bar{X}}$
5. 定义拒绝 $H_{0}$的拒绝域: $\color{red}{样本均值一般符合均值为\mu的正态分布，如果假设成立，\bar{X}落在50附近的概率大。于是提出拒绝域，比如小于48.5或大于51.5}$
6. 根据样本，计算检验统计量的值: $\color{red}{计算 \bar{x}}$
7. 判断是否拒绝: $\color{red}{如果\bar{x}在拒绝域内，拒绝检验假设H_{0}}$

当然假设验证的结论是根据概率得出来的，它会产生两类错误：

		实际情况
		H0正确	H0错误
研究结论	拒绝H0	I类错误	正确
	没有拒绝H0	正确	II类错误

• I类错误
  这类错误危害较大，因为拒绝假设为强结论，如果后续研究、应用基于这个结论，危害不可估量。
  产生原因:
  • 样本中极端数据？
  • 样本太小了？
  • 定义的拒绝域太大了？ 在这个情况下，我们引入显著性水平(Significant Level)的概念，$\color{red}{\alpha = \mathbb{P}\left [ 拒绝H_{0} | H_{0}正确 \right ] }$ ，即发生I类错误的概率，来帮助我们理解拒绝域，可以如本例先给出拒绝域来求得显著性水平，也可以预定义显著性水平来求得拒绝域，都是人为主观预定的，与实际样本数据没有绝对关系。
    在上例中，由于中心极限定理，样本均值服从正态分布，于是我们可以得到显著性水平等式：
    $\alpha = \mathbb{P}\left [ \bar(X)<48.5 | H_{0}正确 \right ] + \mathbb{P}\left [ \bar(X)>51.5 | H_{0}正确 \right ]$
    $前提假设：总体方差\sigma=2.5,样本数量n=10。\color{red}{根据中心极限定理,样本均值会遵从方差为\frac{\sigma^2}{n}的正态分布}。\frac{\sigma^2}{n}=\frac{2.5^2}{10}=0.625,于是方差为\sqrt{0.625}=0.79。$
    $结合检验假设总体均值\mu=50 转化为标准正态分布变量求概率： 小于\frac{48.5-50}{0.79} 和 大于\frac{51.5-50}{0.79}$
    $\alpha = \mathbb{P}( Z < -1.90 ) + \mathbb{P}( Z > 1.90 ) 查表得 = 0.0287 + 0.0287 = 0.0574$
    （当样本数量n变大，样本均值们所遵从的正态分布$\frac{\sigma^2}{n}$的方差变小，均值们会更向中间集中，由同样的拒绝域而求得的显著性水平$\alpha$会变小，即发生I类错误的可能性变小）
• II类错误
  这类错误发生比较普遍，H0错误的情况下，没有拒绝H0。主要是实验设计上面的问题。此类错误危害较小，因为结果为不能拒绝H0为弱结论，并不等于H0正确，只是我们没有足够证据证明H0不正确。 我们引入概念$\color{red}{\beta = \mathbb{P}\left [ 没有拒绝H_{0} | H_{0}错误 \right ]}$。
  比如H0错误，总体均值其实是52,这就相当于在总体均值为52的情况下，求样本均值落在48.5到51.5区间的概率, 即 $\beta = \mathbb{P}(48.5 \leq \bar{X} \leq 51.5 \quad 当\mu=52 )$
  $在同样的前提假设下：总体方差\sigma=2.5,样本数量n=10，我们可以根据中心极限定理获得样本均值的正态分布的方差没有变依然为0.79。$
  $转化为标准正态分布变量时，由于\mu变为52，变成大于\frac{48.5-52}{0.79} 和 小于\frac{51.5-52}{0.79}$ $\beta = \mathbb{P}( -4.43 < Z < -0.633 ) = \Phi(-0.63) - \Phi(-4.43) = 0.2643 - 0 = 0.2643$
  但是当$真正的\mu=50.5,n=10,\sigma=2.5的情况下,$
  $\beta = \mathbb{P}( \frac{48.5-50.5}{0.79} < Z < \frac{51.5-50.5}{0.79} ) = \mathbb{P}( -2.53 < Z < 1.27 ) = \Phi(1.27) - \Phi(-2.53) =0.8980 - 0.0057 = 0.8923$
  在真正的总体均值距离H0假设的总体均值比较近的时候，我们有很大的几率不会拒绝H0。

P值(P-Value)

现在我们有了样本数据，我们可以求得假设H0正确的概率，即为P值。
在上例中：求得样本均值$\bar{x}$至少51.8时,然后我们计算H0:$\mu=50$正确的概率P值。
$根据分布，求得 \mathbb{P}[\bar{X} \leq 51.8 | H_{0}正确]=0.0113$ 因为这是一个Two-sided P-value问题, 这只是一边的情况，因为正态分布是对称的，于是我们判断$P值 = 0.0113 + 0.0113 < \alpha$。于是当我们选择$\alpha=0.05$的时候，拒绝零假设H0。

One-sided还是Two-sided取决于备择假设，备择假设取决于实际问题。一般来讲我们设计假设验证都是想要去拒绝零假设H0，我们关心的其实是备择假设H1，不等于，还是大于或者小于。比如检验新配方是否有改良，数据越高越好时，我们只关心H1:$\mu>\mu_{0}$。
零假设H0: $\mu=\mu_{0}$
样本均值分布: $Z_{0}=\frac{\bar{X}-\mu_{0}}{\sigma/\sqrt{n}}$

备择假设	P值	假设拒绝条件
$H_{1}: \mu \neq \mu_{0}$	$P=2[1-\Phi(|z_{0}|)]$	$z_{0}>z_{\alpha/2} or z_{0}<z_{-\alpha/2}$
$H_{1}: \mu > \mu_{0}$	$P=1-\Phi(z_{0})$	$z_{0}>z_{\alpha}$
$H_{1}: \mu < \mu_{0}$	$P=\Phi(z_{0})$	$z_{0}<-z_{\alpha}$

均值的置信区间 Confidence Interval on the Mean

有时候，根据样本均值，光给出点估计是不够的，我们想要的一个区间，比如真实值有95%的概率落在[48，52]。
置信区间体现了这个参数的真实值有一定概率落在测量结果的周围的程度。比如一个Two-sided区间$\mathbb{P}[L \leq \Theta \leq H]=1-\alpha$
其中$1-\alpha$为置信系数confidence coefficient，即真实值落在[L,H]范围内的概率。
也有单边One-sided区间：$\mathbb{P}[L \leq \Theta ]=1-\alpha 和 \mathbb{P}[\Theta \leq H]=1-\alpha$
当我们拿到一个样本，在给定显著性水平（Significant Level)以后，我们就可以通过计算求得置信区间 Confidence Interval的范围。这个范围由样本数据和显著性水平决定，和假设检验H0无关。当我们求得置信区间的值，根据H0是否落在置信区间，可以判断是否拒绝假设检验H0。
方差已知，或者方差未知样本数量大于30的情况下，公式：$\bar{x}-\frac{z_{\alpha/2}\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+\frac{z_{\alpha/2}\sigma}{\sqrt{n}}$
方差未知，样本数量小于30的情况下，公式：$\bar{x}-\frac{t_{\alpha/2,n-1}s}{\sqrt{n}} \leq \mu \leq \bar{x}+\frac{t_{\alpha/2,n-1}s}{\sqrt{n}}$

单个样本问题主要有以下几种情况

在总体方差已知的情况下，推测总体均值

以上的例子就是基于方差已知的情况。对假设的总体方差进行z-test。 这种情况现实问题中比较少见。
根据中心极限定理，样本均值遵从标准正态分布。

z-test

根据中心极限定理: $Z=\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}$ 服从标准正态分布

验证：
$H_{0}: \mu = \mu_{0}$
$H_{1}: \mu \neq \mu_{0}$
测试的统计量:
$Z_{0}=\frac{\bar{X}-\mu_{0}}{\sigma/\sqrt{n}}$
检验方式：1.P值 2.给定显著性水平 3.置信区间

置信区间 CI公式：$\bar{x}-\frac{z_{\alpha/2}\sigma}{\sqrt{n}} \leq \mu \leq \bar{x}+\frac{z_{\alpha/2}\sigma}{\sqrt{n}}$

在总体方差未知的情况下，推测总体均值

总体方差未知的情况下，如果样本数量大于30，S和$\sigma$的差别比较小，根据中心极限定理均值也更趋向于正态分布。我们可以将样本方差S来近似总体方差$\sigma$直接用于z-test。
可是当样本数量小于30，z-test的误差会比较大。在总体分布为正态分布时，我们可以用到t分布，进行t-test。
t分布：根据小样本来估计呈正态分布且方差未知的总体的均值。
t分布的概率密度函数为：$f(x)=\frac{\Gamma (\frac{k+1}{2})}{\sqrt{k\pi} \Gamma (\frac{k}{2})}(1+\frac{x^2}{k})^{-\frac{k+1}{2}}, x\in \mathbb{R}$。
使用中需要查询t分布临界值表,用自由度k和显著性水平$\alpha$来查询拒绝H0的样本均值临界值。
t分布和正态分布的关系如下图：当自由度k变大，即样本数量变大时，t分布越来越向中间集中，越来越靠近正态z分布。正态分布是t分布的极限状态。

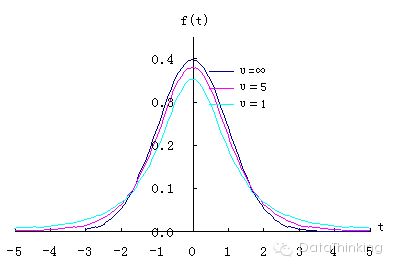
t-test

当$X_{1},...X_{n}服从从正态分布，T=\frac{\bar{X}-\mu}{S/\sqrt{n}}$ 服从t分布

验证：
$H_{0}: \mu = \mu_{0}$

测试的统计量:
$T_{0}=\frac{\bar{X}-\mu_{0}}{S/\sqrt{n}}$ 服从t分布
检验方式：1.P值 2.给定显著性水平 3.置信区间

置信区间 CI公式：$\bar{x}-\frac{t_{\alpha/2,n-1}s}{\sqrt{n}} \leq \mu \leq \bar{x}+\frac{t_{\alpha/2,n-1}s}{\sqrt{n}}$

变量呈正态分布情况下，推测总体方差

首先，变量必须是符合正态分布的。
定理：若n个相互独立的随机变量$X_{1}，X_{2}，...,X_{n}$服从标准正态分布，未知均值$\mu$，未知方差$\sigma^{2}$，则：
$X^{2}=\frac{(n-1)S^{2}}{\sigma^{2}}$
服从自由度为n-1的卡方分布（chi-square distribution）。

chi-square distribution

因为变量呈正态分布，所以$X^{2}=\frac{(n-1)S^{2}}{\sigma^{2}}$ 服从卡方分布

验证：
$H_{0}: \sigma^{2} = \sigma_{0}^{2}$

测试的统计量：
$X_{0}^{2}=\frac{(n-1)S^{2}}{\sigma_{0}^{2}}$
检验方式：1.P值 2.给定显著性水平 3.置信区间

置信区间 CI公式：$\frac{(n-1)s^{2}}{X^{2}_{\alpha/2,n-1}} \leq \sigma^{2} \leq \frac{(n-1)s^{2}}{X^{2}_{1-\alpha/2,n-1}}$

卡方分布临界值表

二项分布情况下，推测比例

z-test

根据中心极限定理,$Z = \frac{X-np}{\sqrt{np(1-p)}}，其中\mu=np,\sigma^{2}=np(1-p)$

验证：
$H_{0}: p = p_{0}$

测试的统计量:
$Z_{0} = \frac{X-np_{0}}{\sqrt{np_{0}(1-p_{0})}}$
检验方式：1.P值 2.给定显著性水平 3.置信区间

置信区间 CI公式：$\hat{p}-z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \leq p \leq \hat{p}+z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$

推测总体分布

• Probability plotting 概率图（主要用来判断正态分布，对数正态分布，威布尔分布） 一般我们可以用样本数据画一个正态概率图。如果这组实数服从正态分布，正态概率图将是一条直线。

  from scipy import stats
  import matplotlib.pyplot as plt
  # generate random numbers
  x = stats.norm.rvs(size=50)
  # probability plot
  res = stats.probplot(x, plot=plt)
  

• Chi-Square Goodness of Fit Test 卡方检验

双样本情况

在总体方差已知的情况下，推测两个分布均值的差别

两个分布的总体均值的差别为：$\mu_{1}-\mu_{2}$,因为中心极限定理两个样本均值分别服从正态分布，有意思的是，两个正态分布的差值是另外一个正态分布（推导）均值为$\mu_{1}-\mu_{2}$，方差为$\frac{\sigma_{1}^{2}}{n_{1}}-\frac{\sigma_{2}^{2}}{n_{2}}$。
即$Z=\frac{\bar{X_{1}}-\bar{X_{2}}-(\mu_{1}-\mu_{2})}{\sqrt{\sigma_{1}^{2}/n_{1}-\sigma_{2}^{2}/n_{2}}}$ 服从标准正态分布,于是我们可以使用Two-sample z-test了。

Two-sample z-test

基于中心极限定理和两正态分布的和/差是另外一个正态分布

验证：
$H_{0}: \mu_{1}-\mu_{2} = \Delta_{0}$

测试的统计量： $Z_{0}=\frac{\bar{X_{1}}-\bar{X_{2}}-\Delta_{0}}{\sqrt{\sigma_{1}^{2}/n_{1}-\sigma_{2}^{2}/n_{2}}}$

在总体方差未知的情况下，推测两个分布均值的差别

若样本数量n1,n2大于30，则使用样本方差近似总体方差，使用上面的Two-sample z-test。 若样本数量较少，我们要求总体分布为正态分布，然后用t分布求解验证假设和置信区间。 然后根据方差分两种情况：

• 两个方差相等$\sigma_{1}^{2} = \sigma_{2}^{2}$，使用Pooled t-Test

  验证: $H_{0}: \mu_{1}-\mu_{2} = \Delta_{0}$

  测试的统计量： $T_{0}=\frac{\bar{X_{1}}-\bar{X_{2}}-\Delta_{0}}{S_{p}\sqrt{1/n_{1}-1/n_{2}}}$ t分布的自由度：n1+n2-2。
  其中，$S_{p}^{2}=\frac{(n1-1)S_{1}^{2}+(n2-1)S_{2}^{2}}{n1+n2-2} \quad （S_{p}是两个样本方差的加权平均。）$

• 两个方差不等$\sigma_{1}^{2} \neq \sigma_{2}^{2}$，使用Welch’s t-Test

  验证：$H_{0}: \mu_{1}-\mu_{2} = \Delta_{0}$

  测试的统计量： $T_{0}^{*}=\frac{\bar{X_{1}}-\bar{X_{2}}-\Delta_{0}}{\sqrt{S{1}^{2}/n_{1}-S{2}^{2}/n_{2}}}$
  t分布的自由度公式比较复杂：$v=\left \lfloor \frac{(\frac{S_{1}^{2}}{n1}+\frac{S_{2}^{2}}{n2})^{2}}{\frac{(S_{1}^{2}/n1)^2}{n1-1} + \frac{(S_{2}^{2}/n2)^2}{n2-1} } \right \rfloor$

配对样本t检验 Paired t-Test

有些样本值可以成对获取，可以做Paired t-Test,一般来说效果比2-sample t-Test的更好，因为后者会包含一些各个观察间的独立变化。
定义：
$D_{i} = X_{1i}-X_{2i} for i=1,...,n$
$\mu_{D} = E(X_{1}-X_{2})=\mu_{1}-\mu_{2}$

One-sample t-Test

验证：
$H_{0}: \mu_{D} = \Delta_{0}$

测试的统计量:
$T_{0}=\frac{\bar{D}-\mu_{0}}{S_{D}/\sqrt{n}}$ 服从t分布

两个正态分布变量的总体方差是否相等

两个正态分布变量，于是$X^{2}=\frac{(n-1)S^{2}}{\sigma^{2}}$服从卡方分布。
由卡方分布的定义：$F=\frac{W/u}{Y/v},W为自由度u的卡方分布，Y为自由度v的卡方分布。$
我们可以得出：$\frac{S_{1}^{2}/\sigma_{1}^{2}}{S_{2}^{2}/\sigma_{2}^{2}}服从F_{n_{1}-1,n_{2}-1}$

F-Test

验证：
$H_{0}: \sigma_{1}^{2} = \sigma_{2}^{2}$

测试的统计量:
$F_{0}=\frac{S_{1}^{2}}{S_{2}^{2}}$

置信区间 CI公式：$\frac{s_{1}^{2}}{s_{2}^{2}}f_{1-\alpha/2,n_{2}-1,n_{1}-1} \leq \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}} \leq \frac{s_{1}^{2}}{s_{2}^{2}}f_{\alpha/2,n_{2}-1,n_{1}-1}$

F分布临界值表

多样本情况（ANOVA）

ANOVA(Analysis of Variance), 用于两个及两个以上样本均值差别的显著性检验，判断他们来自的总体均值是否相同，也是基于F-Test，不过分子和分母与上面双变量情况下有所不同。
大致意思是：$F = \frac{组间方差}{组内方差}$

例子：
我们有a组数据，每组n个。

• 求得每组均值，然后求得这a个均值间的方差，为SST。自由度为a-1。
• 求得每组内的方差的和,为SSE。自由度为a(n-1)。

测试的统计量: $F_{0} = \frac{\frac{SST}{(a-1)}}{\frac{SSE}{a(n-1)}}$

用F值与其临界值比较，推断各个样本是否来自相同的总体。

（基于假设，变量为正态分布，每组间相互独立且方差相同）