简介
时间序列预测是非常常见的,比如:每天的销售量,每小时的地铁人流量。 直接看Python代码
形式
- 内生时间序列预测(单变量)<= 本文内容
很多时候我们很难找到影响观测值的元素,或者找到了关联元素却找不到数据,这个时候我们可以使用观测值的历史数据来对它本身进行预测。
预测值的变化与时间有关,长期呈现上升或者下降趋势,很多的时间序列出现季节性或者周期性趋势的变化。 - 外生时间序列预测(因果关系,多变量)
主要技术
- Overall Trend models 整体趋势
- Smoothing models 平滑模型
- Decomposition models 分解模型
- ARIMA models ARIMA 模型 <= 本文内容
ARIMA(p,d,q)
ARIMA可以分成三个部分:AR, I, MA.
Auto-Regressive (AR) ~ Regression on itself ( y on y history)
自回归模型:设若时间序列(或随机过程)的任一元素Yt与其前期元素(Yt-1、Yt-2 … Yt-p等)之间存在着某种线性关联,则我们可以根据该时间序列的既往观测值来预测其未来的取值。
\[ \hat{y_{t}} = a_{0} + a_{1}y_{t-1} + a_{2}y_{t-2} + … +a_{p}y_{t-p} \]
p值决定了用几个自变量
- 当 p=1:
- 当 p=2:
我们可以看到这是一个简单线性回归模型(SLR),我们要保证它的自变量和因变量不能有自相关。
基于假设 :
- Linear relationship between successive values
Yt与Yt-1,Yt-2...之间具有线性关系。(毕竟这是线性回归模型)
- Yt is a Stationary process
Yt是平稳的。时间序列的行为并不随时间改变!!! (不然怎么找规律)
- Errors are normal and independent
误差呈正态分布,相互独立。
Integration (I)
可是真实数据,一般都是不平稳的。它可能有趋势,或者值和变化方向随机变化。
我们用一个步骤Regular differencing (RD)来获得平稳的序列。(主要是消除趋势)
- ( Order):
- ( Order):
有的序列需要一阶differencing变平稳,有的需要进行二阶differencing才能平稳,一般不会超过二阶.
为了更方便的写表达式,在这里我们引入 Backshift Operator (B):
定义 ,于是
于是一阶的Differencing表示为:
\[ {y}’_{t}=y_{t}-y_{t-1}=y_{t}-By_{t}=(1-B)y_{t} \]
二阶Differencing表示为:
\[ {y}’'_{t}=(1-B)^{2}y_{t} \]
下面分别是原序列,一阶Differencing序列和二阶Differencing序列,我们可以看到,这个序列经过了二阶Differencing的曲线变得平稳了。
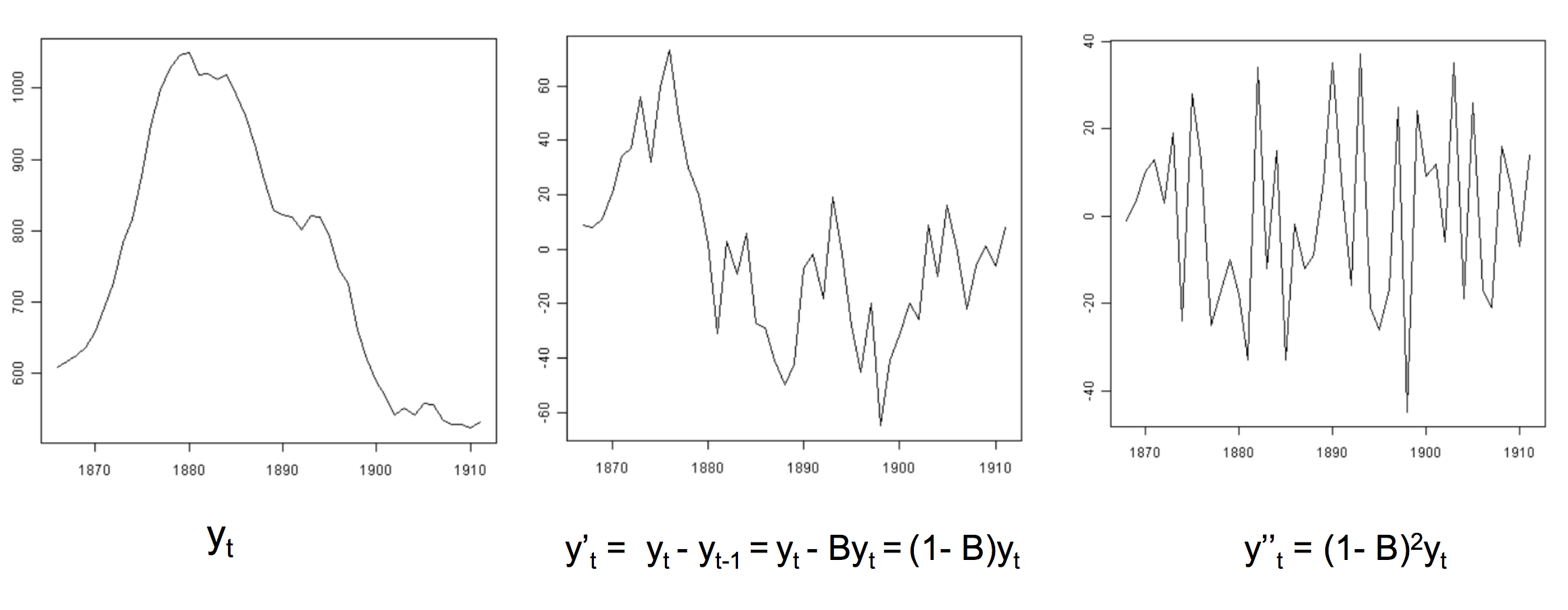
一般上图足够判断一个序列是否平稳。我们可以用ACF和PACF图容易的看出一个序列的不平稳。
Moving Average (MA) Models
移动平均模型: